Ecuaciones cuadraticas

Esto es una ecuación cuadrática:

(a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.)

La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes                  VARIABLE: es un símbolo para un número que todavía no conocemos. Normalmente es una letra como x o y. COEFICIENTE: es un número que está multiplicando a una variable

Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un cuadrado (en otras palabras x2).

Ejemplos de ecuaciones cuadráticas:

		En esta a=2, b=5 y c=3
		Aqui hay una un poco más complicada: ¿Dónde está a? En realidad a=1, porque normalmente no escribimos "1x2" b=-3 ¿Y dónde está c? Bueno, c=0, así que no se ve.
		¡Ups! Esta no es una ecuación cuadrática, porque le falta el x2 (es decir a=0, y por eso no puede ser cuadrática)

¿Qué tienen de especial?

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática: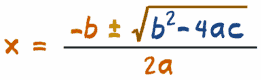

	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!
	La parte azul (b2 - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios .

Solución

Para resolverla, sólo pon los valores de a,b y c en la formula cuadrática haz los cálculos.

Ejemplo: resuelve 5x² + 6x + 1 = 0

Fórmula cuadrática: x = [ -b ± √(b²-4ac) ] / 2a
Los coeficientes son: a = 5, b = 6, c = 1
Sustituye a,b,c: x = [ -6 ± √(6²-4×5×1) ] / 2×5
Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10

Respuesta: x = (-0.2) y (-1)
(Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)

Si quieres una mejor explicacion, aquí te dejo este vídeo, en el que se te explicara como resolver una ecuación cuadrática con la formula ya expuesta ;) :

¿Cómo resolver una ecuación cuadrática por factorización?

Para resolver ecuaciones de segundo grado o cuadrática por factorización (o también llamado por descomposición en factores), es necesario  que el trinomio de la forma  ax² + bx + c = 0 sea factorizable por un término en común o aplicando un producto notable.
Para esto,
1° Deberás simplificar la ecuación dada y dejarla de la forma ax² + bx + c = 0.
2° Factorizar el trinomio del primer miembro de la ecuación, para obtener el producto de binomios.
3° Igualar a cero cada uno de los factores, esto lo podemos realizar, ya que sabemos que si un producto es igual a cero, uno de sus multiplicandos o ambos, son iguales a cero.  Luego, se resuelven las ecuaciones simples que se obtienen de este modo.
Ejemplo:
a) Resuelve por factorización la ecuación X² - x - 6 = 0
- En este caso la ecuación se encuentra simplificada, entonces factorizamos e igualamos a cero los factores;

Respuesta: Las raíces de la ecuación son -2 y 3.

Aquí te dejo mi amigo mas explicado dicho método por medio de este vídeo ;) te servirá de mucho:

Gracias por tu visita! Espero te haya sido útil este blog ;) 

No olvides dejar tu comentario!

Realizado por: Iván Alejandro Sanherman Regalado  104