Modelos aritméticos o algebraicos
MONOMIOS
es una expresión algebraica en la que se
utilizan exponentes naturales de variables literales que constan de un solo
termino, un numero llamado coeficiente. Las únicas operaciones que aparecen
entre las letras son el producto y la potencia de exponentes naturales. Un
monomio es una clase de polinomio con un único termino.
Un término algebraico consta de tres partes
principales:
a) Un
número real ( R ), mejor conocido en
el álgebra como coeficiente que multiplica a la variable o literal.
b) Una
variable o literal, que representa a la magnitud de estudio.
c) Un
exponente, que indicara las veces que se va a operar a la variable por medio de
la multiplicación por sí misma, el cual siempre será un numero natural (N) que indica el grado del monomio. En
caso de que exista más de una variable, el grado se determina sumando todos los
exponentes.
De manera general, un monomio tiene la forma:
Rxᶰ
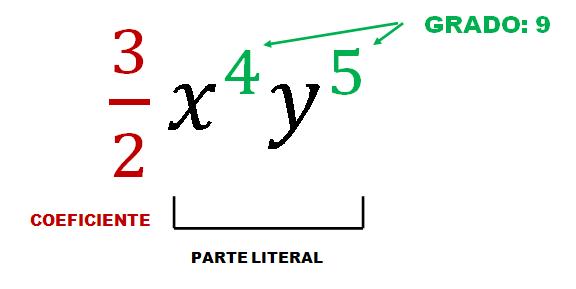
A la expresión anterior se le denomina monomio,
ya que solo es un término algebraico. Cabe aclarar que en esta expresión
algebraica las variables no se ubicaran en el denominador, ya que en este caso
el término dejaría de ser un monomio.
 Algunos
ejemplos son:
Algunos
ejemplos son:
·
5a²
·
7m³
·
6n
·
8x²
Polinomios
Cuando los monomios se unen por medio de los
signos de la suma o resta, cambian de nombre y adoptan el nuevo nombre de binomios, en
otras palabras, es una expresión algebraica formada por la suma o resta de dos
monomios. Trinomios
si tienes tres monomios, y a partir de cuatro términos en adelante reciben el
nombre de polinomios.
Un polinomio es una expresión matemática
constituida por un conjunto finito de variables y constantes, utilizando
únicamente las operaciones aritméticas de suma, resta y multiplicación así como
exponentes enteros positivos. En términos más precisos, es una relación de
monomios, o una sucesión de sumas y restas de potencias enteras de una o de
varias variables indeterminadas.


Binomio Trinomio Polinomio
Compuesto de
Si tiene tres A
partir de
2 binomios. monomios. cuatro términos.
El grado de estas expresiones se determina
con el exponente máximo de algunos de los monomios, por ejemplo:
2t+3
|
Es un binomio de primer
grado.
|
2t²+5t3
|
Es un trinomio de segundo grado.
|
a³+3a²b5ab²+1
|
Es
un polinomio de tercer grado respecto de la variable a.
|
Les dejo este vídeo por si tienen alguna duda ;) :
Realizado por la alumna Claudia Alejandra Hernández Peláez
Grupo:
104
Cobaev
12 Medico “Enrique Herrera Moreno”
Martes
25 de octubre de 2016